my blog: gerak harmonik sederhana

Suatu obyek yang bergerak sepanjang sumbu-X dikatakan melakukan gerak harmonic sederhana jika kedudukannya sebagai fungsi dari waktu menurut persamaan
$x(t)=x_{0}+A\cos \left ( \omega t+\varphi \right )$
Obyek tersebut berosilasi (bergetar) di sekitar posisi kesetimbangan x₀. Jika kita memilih posisi kesetimbangan tersebut sedemikian hingga x₀= 0, maka perpindahan x dari posisi kesetimbangan sebagai fungsi dari waktu diberikan dengan persamaan:
$x(t)=A\cos \left ( \omega t+\varphi \right )$
A adalah amplitudo osilasi (getaran), yaitu perpindahan maksimum terjauh obyek dari kesetimbangan, baik kearah x negatif atau positif.
Gerak harmonik berulang-ulang.
Periode T adalah waktu yang diperlukan untuk satu getaran dan kembali ke posisi awal.
Frekuensi anguler ω diberikan dengan
$\omega =\frac{2\pi}{T}$
Frekuensi anguler diukur dalam radian per sekon.
Kebalikan dari periode adalah frekuensi f :
$f=\frac{1}{T}=\frac{\omega }{2\pi}$
Frekuensi diartikan dengan banyaknya getaran dalam satu sekon, satuannya Hertz (1 Hertz = 1/s).
Kecepatan obyek sebagai fungsi dari waktu diberikan dengan
$v(t)=\frac{dx(t)}{dt}=-\omega A \sin \left ( \omega t+\varphi \right )$
dan percepatannya diberikan dengan persamaan
$a(t)=\frac{dv(t)}{dt}=-\omega^2A \cos \left ( \omega t+\varphi \right )=-\omega^2x$
Besaran φ merupakan konstanta fase, besarnya ditentukan oleh keadaan awal dari obyek. Jika pada saat t=0, obyek berada pada perpindahan maksimum x positif maka φ=0, jika berada pada perpindahan maksimum x negatif maka φ=π. Jika pada saat t=0, obyek sedang bergerak melalui kedudukan setimbangnya dalam arah x negatif maka φ=π/2. Besaran ωt+φ disebut dengan fase.
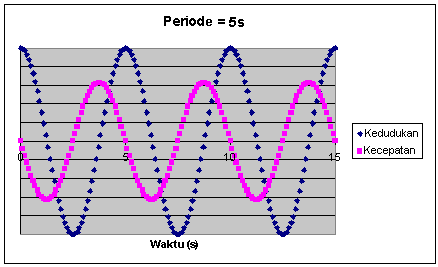
Gambar berikut menunjukkan fungsi kedudukan dan kecepatan sebagai fungsi dari waktu untuk suatu getaran dengan periode 5 s. Amplitudo dan kecepatan maksimum boleh mempunyai satuan sembarang. Kedudukan dan kecepatan tidak sefase. Kecepatan bernilai nol pada perpindahan maksimum, dan perpindahan bernilai noi pada kekajuan maksimum.

Untuk gerak harmonil sederhana, percepatan a = -ω²x sebanding dengan perpindahan, tapi arahnya berbeda. Gerak harmonik sederhana adalah gerak dipercepat. Jika suatu obyek melakukan gerak harmonik sederhana, suatu gaya tentunya sedang bekerja pada obyek tersebut. Gaya tersebut adalah
F = ma = -mω²x .
Ini sesuai dengan hukum Hooke, F = -kx, dengan k = mω².
$F=ma=m\frac{d^2x}{dt^2}$
dengan F = -kx, sehingga diperoleh persamaan differensial tingkat kedua